Stability of Runge-Kutta Method

강좌: 수치해석

안정성

시간 간격에 따라 정확도 뿐 아니라 알고리즘이 발산할 수 있다. 이는 수치 안정성과 관계된다.

안정성을 분석하기 위해 Model problem을 생각한다.

\[ \frac{dy}{dt}=f(y,t) = f(y_0, t_0) + (t-t_0)f_t + (y - y_0) f_y + ... = \lambda y + Others \]

\[ \frac{dy}{dt}= \lambda y, ~~~~\lambda = \lambda_R + i \lambda_i \]

\(\lambda_R < 0\) 인 경우 이 미분방정식은 해가 제한되어 (bounded) 있다.

Sympy

sympy 는 Symbolic Math 프로그램으로 수식 연산을 지원한다.

이를 이용하면 수식 전개에 활용할 수 있다.

%matplotlib inline
from matplotlib import pyplot as plt

import numpy as np

plt.style.use('ggplot')
plt.rcParams['figure.dpi'] = 150

import sympy as sy

# Symbolic Math
lam = sy.Symbol('lambda')
h = sy.Symbol('h')
t = sy.Symbol('t')
y = sy.Symbol('y')


# Define model function y'= lambda y
def ff(t, y):
    return lam*y

Explicit Euler Method

# Expression
expr = sy.simplify((y + h*ff(t, y))/y)

print(expr)

# Sig
z = sy.Symbol('z')
sigf = sy.lambdify(z, expr.subs(h*lam, z), 'numpy')

# Make grid
xx = np.linspace(-3, 3, 201)
yy = np.linspace(-3, 3, 201)
X, Y = np.meshgrid(xx, yy)
z = X + Y*1j

# Amplication factor of Explicit Euler (z=lambda h)
sig = sigf(z)

# Same scale of x and y
plt.axis('equal')

# Stability region
plt.contourf(X,Y,abs(sig), levels=[0, 1])

# Title
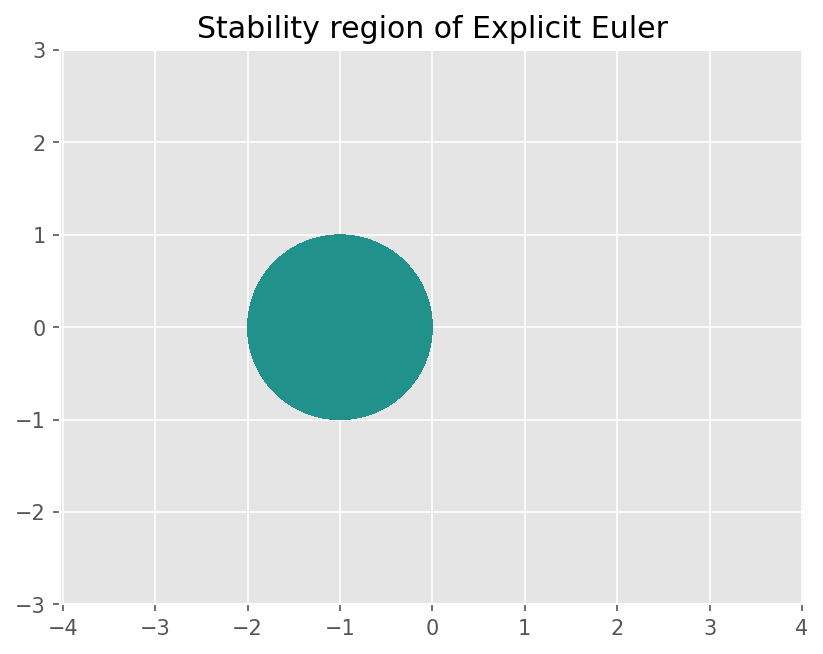
plt.title('Stability region of Explicit Euler')

h*lambda + 1

Text(0.5, 1.0, 'Stability region of Explicit Euler')

2nd-order Runge-Kutta Method

# Coefficient for Heun's
c2, a21 = 1, 1
b1, b2 = 0.5, 0.5

# Coefficient for Midpoint
#c2, a21 = 1/2, 1/2
#b1, b2 = 0.0, 1.0

k1 = ff(t, y)
k2 = ff(t + c2*h, y+ h*a21*k1)

# Factor expression
expr = sy.simplify((y+ h*(b1*k1 + b2*k2)) / y)
print(expr)

# Sig
z = sy.Symbol('z')
sigf = sy.lambdify(z, expr.subs(h*lam, z), 'numpy')

# Make grid
xx = np.linspace(-3, 3, 201)
yy = np.linspace(-3, 3, 201)
X, Y = np.meshgrid(xx, yy)
z = X + Y*1j

# Amplication factor of Explicit Euler (z=lambda h)
sig = sigf(z)

# Same scale of x and y
plt.axis('equal')

# Stability region
plt.contourf(X,Y,abs(sig), levels=[0, 1])

# Title
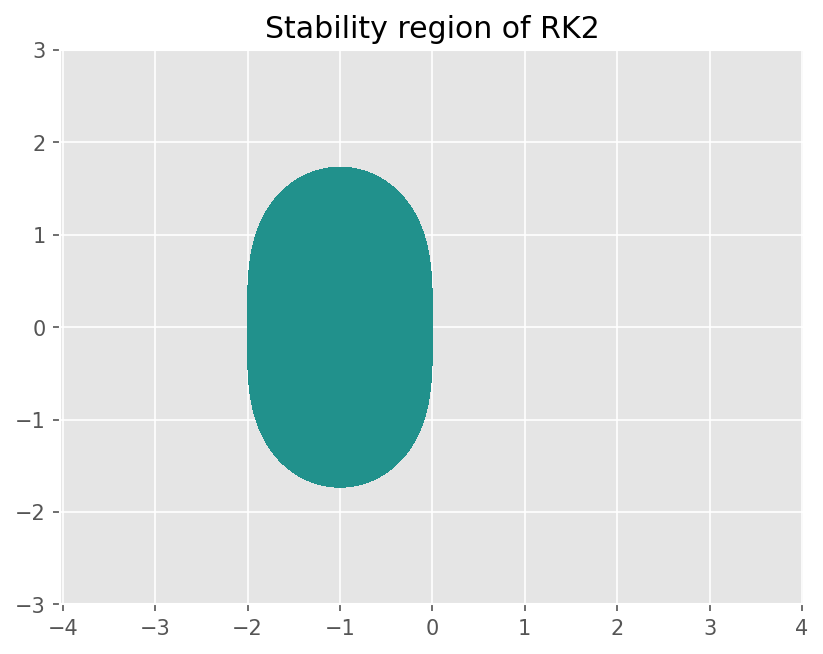
plt.title('Stability region of RK2')

0.5*h*lambda*(h*lambda + 2) + 1

Text(0.5, 1.0, 'Stability region of RK2')

4th-order Runge-Kutta Method

# Coefficient for classical RK4
c2, c3, c4 = 0.5, 0.5, 1.0
a21 = 0.5
a32 = 0.5
a43 = 1.0
b1, b2, b3, b4 = 1/6, 1/3, 1/3, 1/6

k1 = ff(t, y)
k2 = ff(t + c2*h, y+ h*a21*k1)
k3 = ff(t + c3*h, y+ h*a32*k2)
k4 = ff(t + c4*h, y+ h*a43*k3)

# Factor expression
expr = sy.simplify((y+ h*(b1*k1 + b2*k2 + b3*k3 + b4*k4)) / y)
print(expr)

# Sig
z = sy.Symbol('z')
sigf = sy.lambdify(z, expr.subs(h*lam, z), 'numpy')

# Make grid
xx = np.linspace(-3, 3, 201)
yy = np.linspace(-3, 3, 201)
X, Y = np.meshgrid(xx, yy)
z = X + Y*1j

# Amplication factor of Explicit Euler (z=lambda h)
sig = sigf(z)

# Same scale of x and y
plt.axis('equal')

# Stability region
plt.contourf(X,Y,abs(sig), levels=[0, 1])

# Title
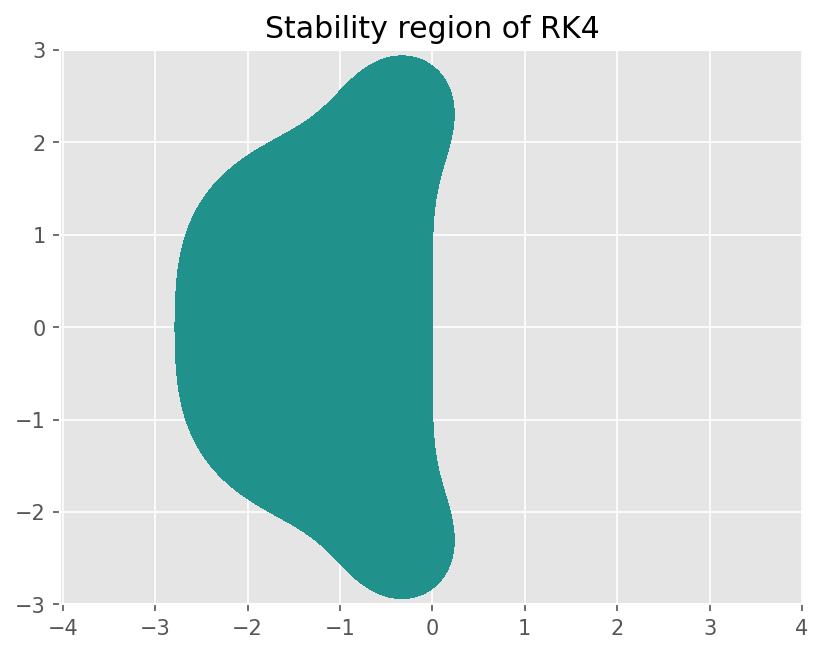
plt.title('Stability region of RK4')

0.0416666666666667*h**4*lambda**4 + 0.166666666666667*h**3*lambda**3 + 0.5*h**2*lambda**2 + 1.0*h*lambda + 1.0

Text(0.5, 1.0, 'Stability region of RK4')